分数除以分数(分数除以分数的意义)
分数除以分数(分数除以分数的意义)

分数除以分数
(bluehouse456 全文整理图解)
今天我们一起来学习人教版六年级上册第三单元分数除法的第二课时一个数除以分数。
现在,让图解我们一起来解决一道实际问题。
小明走了两千米,小红走了5/6千米,谁走的快一些?
看看你能读懂些什么,谁走得快呢?
有道分数同学很快就说出小明走的快,因为两千米大于5/6千米。
这时候有同学反对不对不对,并不知道他们走这些路程所用的时间,所以只有路程是没办法比较快慢的。
这位同学思考问题很全面,看来在比较快慢的问题时,只有路程这一个量是反思不够的。
现在给出了两人所走路程各自所用的时间。
小明2/3小时走了两千米,小红5/12小时走了5/6千米,谁走得快些?
再来比较谁走的快,解决这个问题,你又是怎样想的?
是的,分别求出两个人的速度,然后就可以比较它们的快慢了。
要求视频小明平均每小时走多少千米?如何列算式?
二除以2/3大家一定都是这么想的,用路程除以时间视频等于速度我们并不陌生,那么怎样计算二除以2/3呢?
同学们,分数除以分数练习题,画个图试试吧。
我们一起来看看小婷同学画的视频图。
这个图已经表示出所给的已知条件要求的问题是每小时含义走的路程,也就是一小时走的路程,大家教案想一想,分数除以分数怎么算,一小时走的路程比两千米多还是少?
小雨说,一定是比两千米多,因为一小时比2/3小时时间长数计,所以走的路程也一定比两千米多,分数除以分数怎么除。
你说的很有道理,分数除以分数的计算方法,同学们,你们也是这样想的吗?现在我们确定一小时走的路程要比两千米多,可是在线段图上怎样画出来呢?
小婷计算受到启发练习题,说。
我知道接着怎么画了,2/3小时就是把一小时平均分成三份推导,现在表示出的是其中的两份,所以我先把这条线段平均分成两份,再补充这样的一份,就是一小时所走的路程了,其中的两份表示2/3小时走了两千米。这三份就是我们要解决的问题,一小时走了多少千米?
小婷利用分数的算题意义,根据2/3小时和一小时的关系,把线段图画完整了。
同学们,我们用画图的方式再次理解了题意,明确了要求的问题。现在请你自己尝试着计算吧。
我们一起来算题看看同学们的计算方法。
先来算看看小B的方法,分数除以分数怎样计算。
用两个圆表示二,把每个圆平均分成三份,将其中的两份涂色,这两份就是一个圆的2/3。在这两个圆里,第一个两份涂黄色,第二个两份涂蓝色,第三个两份涂绿色,这两就能够看出二里面有三个2/3,所以二除以2/3等于三。
你们看他用画图的方法,直观的让大家看到二里面有三个2/3,数形结合的方法,确实能够帮助我们解决问题,还有不同的方法吗?
小兵说。
我利用了商不变的性质,把被除数和除数同时乘3/2,乘3/2是为了把除数变成一,被除数变成三。
这样算式就变成了三除以一等于三,分数除以分数原理。
利用商不变的性质,把除数是分数的除法转化成除数是整数的除法来计算,转化思想真是我们的好帮手,还有吗?
小智还有不同的方法。
根据分数与除法的关系,把2/3写成括号二除以三的形式,打开括号时要注意变号等于二除以二,再除三,结果也是什么等于三。大家看又是转化,利用分数与除法的关系,把分数除法转换成整数除法,再进行计算。
看来同学们都具备了用旧知识来解决新问题的含义本领,真棒。
小新,你来说说,在上节课的学习中,我们知道了分数除以整数就等于乘整数的倒数,所以我觉得还可计算以用乘倒数的方法。
同学们,你们看,把除数是整数的计算方法迁移到除数是分数的计算中,这就是类推的方法呀。
屏幕前的同学们,你们是用什么方法计算的呢?相信你们也一定能够应用旧知识来解决新问题。
现在我们一起结合刚才画的线段图,再来看看有什么新的发现100吗?
同学们,一起听听小智的发现,分数除以分数计算题。
我发现在线段图中,2/3小时走的路程是两份,一小时走的路程是三份,那么只要能求出一份走的路程,也就是1/3小时走的路程再乘三,就得到一小时走的路程了。
真的是这样,看来画图不但能帮助我们理解题意,还能助力我们分析问题数计呢,谁意义还有发现呢?
小丽也有发现,我发现方法三中的二除以二就是在求小智所说的一份走的路程,再乘三,求出道一小时走的路程。这个算式和线段图表达题的意思完全一样。
你找到了算式和线段图之间的联系,正好确实是这样,先求一份的路程,然后再求出推导三分的路程。同学们看,二除以二也可以利用上节课的知识,分数除以整数就等于乘整数的倒数,写成二乘1/2的形式。
再想一想,图和算式还有联系吗?
小兵受到了老师的启发,有了新的想法,我想到了,大家看方法四,先求1/3小时走多少千米,因为两个1/3小时走了二千米,所以一个1/3小时走的路程是二千米的1/2,即二乘1/2。再求一小时走多少千米,因为一小时是三个1/3小时,所以一小时走的路程就是1/3的小时走的三倍,即二乘1/2乘三。计算时可以应用乘法结合律,先算1/2乘三等于3/2,这时候算式就等于二乘3/2,也就是方法四,结果等于三。
小兵结合线段图思考出方法四的计算道理,分数除以分数的题100道。
同学们,刚才我们不但过程找到了图和算式之间的联系,还能够发现方法三和方法四其实思路完全相同数计,都是先求一份,再求三份,只是书写方式不同而已。
回顾刚才我们分析的过程,要想计算二除以2/3,可以怎样计算?
可以直接写成是什么二乘3/2等于三千米。
为什么可以写成数计方法二乘3/2?
因为两千米对应着三份中的两份,先求出一份的路程,也就是1/3小时走的路程,列式为二乘1/2。
然后再乘三,求出三份的路程,就是一小时的路程。二乘1/2乘三利用乘法结合律。
把这个算式可以原理整理为二乘3/2。
所以含义教学二除以2/3可以直接写成二乘3/2。
同学们,分数除以分数教案,请你观察这个算式,你能发现什么没变,什么变了?是怎样变化的?
聪明的你们一定发现被除数没有变。
除号算变成了乘号概念。
除数变成了它的倒数。
看到了最后计算的结果,小雨说,二除以2/3的结果是三,真的,分数除以分数的计算题100道,第二大除法算式还可以越除越大呢。我发现这和二除以2/3转化成了二乘3/2有直接的关系。
你真善于思考,前面我们通过比较时间,确定了一小时走的路程会比两千米多,现在通过计算证实了确实多。小雨还发现,多的原因跟除数的大小有直接关系。
通过前面的自主探究,我们求出了小明的速度,那小红的速度呢?要求小红平均每小时走多少千米?应该怎样列算式?
5/12小时是时间,5/6千米反思是路程,分数除以分数教学视频。
还应该用路程除以时间等于速度分数列式为5/6除以5/12。
现在请大家画图并独立计算道,分数除以分数怎么除?,开始吧。
同学们,怎么样?算出来了吗?我们一起来看一下。
5/6除以算5/12等于5/6乘12/5等于两千米。
你们也是这样算的吗?现在老师想问大家,为什么写成乘12/5?
有了前面的经验,先求出1/12小时走了多少千米,就是推导把5/6千米平均分成五份,求一份是多少,也就是求5/6千米的1/5是多少,用5/6乘1/5表示。
再求出这样的12份,就是一小时走了多少千米?
如果用画图的方式再来加深一下理解,应该怎样画呢?
跟着课件演示说一说每一步求的是什么?
画一条线段,表示5/12小时走了5/6千米。
根据5/12小时与一小时的关系,把线段图补充教学完整。
我们要求的问题是,一小时走了多少千米?
先求一份的路程,也就是求出图解1/12小时走了多少千米。
再乘12,就是一小时走的路程。
通过画图,我们清楚了为什么可以把5/6除以5/12转换成5/6乘12/5来进行计算的道理。
再来观察这道分数除以分数的题目,你能发现100什么没变,什么变了?是怎样方法变化的?
是的,被除数没有变,除号教学变成了乘号,除数变成了它的倒数。
现在回到我们的问题,谁走的更快些呢?通过我们的比较,我们知道小明每小时走三千米,小红每小时走两千米,因为三千米大于分数两千米,所以小明走的更快一些。
这样,这道比较快慢的问题我们就解决了。
同学们,在解决问题的过程中,我们研究了整数除以分数,分数除以分数,现在能用自己的理解说一说一个数除以分数的计算题方法吗?
听听他们是怎么说的。
应该就是被除数没有变,除号变成了乘号,除数变成了它的倒数。我觉得就可以这样说,在分数除法中,除以一个数就等于乘这个数的倒数。
我算题补充,分数除以分数推导过程,除数不能为零,除以一个不为零的数等于乘这个数的倒数。
你们说的都很好,后面这位同学说的更严谨,零不能做除数,这样我们就总结出了分数除法的计算方法,除以一个不等于零的数,分数除以分数,等于乘这个数的倒数。
再用自己的含义话题说说,一个数除以分数可以怎样计算呢过程?
理解了计算道理,掌握推导了计算方法后原理,我们再来做两道练习题吧,分数除以分数是什么。
计算下面各题,分数除以分数的图解。
算出来了吗?
答案一样吗?
请问计算时你们注意了什么问题?我想提示大家,可以在计算过程中边约分边计算,这样确保得到的结果是最简分数。
很好的提示,边约分边计算是个好方法,要想提高计算的正确率,一定的练习是必不可少的,所以大家要多积累计算经验分,努力提高自己的计算能力,分数除以分数的含义。
同学们,研究计算是为了更好的解决生活实际问题,在生活中你遇到过这样的问题吗?能解决吗?请看屏幕。
把3/4升橙汁分装在容量是1/4升的小瓶里,分数除以分数的意义,可以装满是什么几瓶?
这道题怎么做呢?算式是3/4除以1/4还是1/4除以3/4呢?
小兵说,我想明白了,3/4升在题目中是长之总量教案,也就是总数。每个小瓶里能装1/4升,也就是每份数,求可以装几瓶,也就是求3/4里面有几个1/4。所以分数除法的数量关系和整数除法的数量关系是一样的,应该用3/4除以1/4等于三瓶。
但是1/4除以3/4,求出的又是什么呢?
你提出了非常有价值的问题,为什么用3/4除以1/4?想清楚了,我们也得弄明白,为什么不能用1/4除以3/4,你们能帮他解答吗?
小鱼说,这道题挺难想的,我还是想借助画图来帮忙把一生橙汁平均分成四份,其中的三份就是3/4升,1/4升的小瓶刚好是其中的一份,所以3/4除以1/4,求的是3/4里面有三个1/4,可以装三瓶。
1/4除以3/4,求的分是1/4升是3/4升的几分之几和这道题意义完全不同,所以不能这样是什么列式。
分析的很有道理,图真是个好帮手,让我们明白了3/4除以1/4和1/4除以3/4这两个算式的含义,最终我们确定了这道题除以应该用3/4除以1/4等于三瓶,这位同学能够结合除法的意义进行分析,并且分析的有理有据。
要提高我们的分析能力,这些严谨的思考过程真是必不可少啊,分数除以分数的教学反思。
同学们,这节课就要结束了,说说你们有什么收获呢?一起听听他们的原理收获。我学会了分数除法的计算方法,分数除法可以转化成分数乘法来计算。
我还明白了为什么可以这样算,画图能帮我理解计算的道理,解决问题中列算式前一定要先理清思路。说的真好,看来大家在知识上、方法上都有了一定的收获。学习中我们不仅100要知其然,还要知其所以然,努力探究方法背后的道理。相信屏幕前的你们也有自己的收获,分数除以分数的概念,课下可以跟你的家人分享。
今天我们学习了分数除法的第二课时,具体内容在数学书第30页和第31页。
同学们课后完成数学书第31页做一做的第二题和数学书第33页练习七的第一题,应用计算方法提高计算能力,这节课我们就上到这里,同学们再见。
-

- 软科排名是什么意思(软科、CNUR、武书连、校友会哪个排名更靠谱)
-
2023-05-25 03:47:59
-

- 谢霆锋王菲发文宣布产女(51岁王菲被曝冒生命危险产子)
-
2023-05-25 03:45:43
-

- 巴基斯坦为什么和中国这么好(中国和巴基斯坦关系为什么这么好)
-
2023-05-25 03:43:27
-

- 全球100强城市gdp排名(100个繁荣城市中国入围了10个)
-
2023-05-25 03:41:12
-

- 这3类人不建议去十三陵游玩(十三陵风景区旅游攻略)
-
2023-05-25 03:38:55
-

- 我国下月正式取消小区物业费(2022年物业费将“全面停收”?)
-
2023-05-25 03:36:39
-

- 长平之战的交战双方是谁(带你了解不一样的长平之战)
-
2023-05-25 03:34:24
-

- 村镇银行事件最新进展(河南村镇银行400亿大案已逮捕234人)
-
2023-05-25 03:32:08
-

- 阖家幸福的意思(“阖家”与“合家”的区别在哪)
-
2023-05-25 03:29:52
-

- 鲜榨果汁配方表(10款鲜榨果汁做法简单)
-
2023-05-25 03:27:36
-

- 美股创 9 个月新高 华尔街激辩:“重大突破”还是“牛市陷阱”?
-
2023-05-24 09:30:44
-

- 玩家优越感哪有挣钱重要,索尼大谈移植 PC 的正确性
-
2023-05-24 09:28:28
-

- 蜘蛛侠 X 蜘蛛侠,索尼 Mini LED 电视 X95EL 纵横潮酷视听体验
-
2023-05-24 09:26:12
-

- 微信“刷手”新功能,居然九年前就已诞生!
-
2023-05-24 09:23:56
-

- 美国,这次又“放鸽子”?
-
2023-05-24 09:21:40
-

- 评测华为随行 WiFi 3 Pro 天际通版:高速传输,4G 信号随身行
-
2023-05-24 09:19:25
-

- 乌军突然攻入俄境内,这件事很不简单
-
2023-05-24 09:17:09
-

- 不到 10 万元,钇为 3 开启预售,海豚的劲敌来了?
-
2023-05-24 09:14:53
-

- 生活不在「别处」,在每一个被记录的「当下」
-
2023-05-24 09:12:36
-

- 王者荣耀青铜到王者一共多少星段位
-
2023-05-24 09:10:21





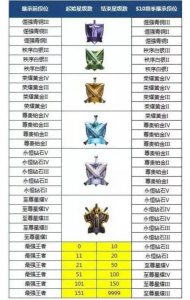 王者荣耀青铜到王者一共多少星段位
王者荣耀青铜到王者一共多少星段位 鲜榨果汁配方表(10款鲜榨果汁做法简单)
鲜榨果汁配方表(10款鲜榨果汁做法简单)